![[PukiWiki] [PukiWiki]](image/ibisforest.png)
本書は,Christopher M. Bishop 著「Pattern Recognition and Machine Learning」の日本語版です.
ベイズ理論に基づく統計的予測技術は,計算アルゴリズムの開発と計算機の性能向上によって,急速に進展しました.本書は,このベイズ理論の観点で統一的に整理された視点で,各種の機械学習・パターン認識の理論や手法を解説しています.
本書は,確率入門・決定理論・回帰問題・識別問題のような基本的で平易な話題から始まっています. これらの基本をふまえた上で,90年代に登場したサポートベクトルマシンやブースティングといった手法,機械学習アルゴリズムの適用範囲を広げたカーネルトリックやグラフィカルモデル,およびベイズ理論の実用化にあたって不可欠だったMCMCや変分ベイズといった高度な話題までを学ぶことができます.
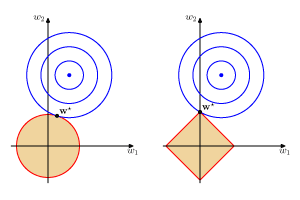
機械学習・パターン認識の本は数式による説明だけになりがちです.本書はこうした形式的な説明に加えて,図を用いた直観的な説明も加えています.例えば,左の図3.4をみると,円で表された分布が,影付きの部分(解の存在範囲)と接触するとき,右側の方が「角」で接触しやすいことは視覚的に分かります.このことから,w の多くの要素が 0 になりやすいことが直観的に理解できるでしょう.こうしたイメージを伴った理解は,機械学習手法を応用問題に適用するときや,新たなアイデアを創出するときに役立つことでしょう.さらに,多くの図をカラーで収録しましたので,とても見やすくなっています.
本書は演習問題も豊富で,400問以上収録されています.これらの問題は自身の理解度を確認するのに役立つでしょう.
機械学習の大きな枠組みと,確率と情報理論の基本について学びます.
まず,パターン認識・機械学習の基本的な枠組みである教師あり学習や教師なし学習などを紹介します. ベイズの定理,期待値,分散などの確率の基礎を学んだあと,最尤推定などの基本的な推定手法に加えて,交差確認や次元の呪いといった重要な注意事項について述べます. 損失関数を最小にするという決定理論に続き,エントロピーやカルバック-ライブラーダイバージェンスなどの情報理論の基礎について述べます.
これらの分布について,ベイズ推定をしたときの事前分布や事後分布の具体的な形を導きます. また,逐次推定,指数型分布族,共役事前分布,無情報事前分布などの確率分布に関する事項も合わせて述べます. 最後に,カーネル密度推定や最近傍法などのノンパラメトリック手法を紹介します.
基本的な線形回帰から始め,その逐次推定や,正則化を導入したリッジ回帰,バイアス-バリアンスなどの発展的な内容を取り上げます. さらに,こうした最尤推定による方法に加えて,ベイズ推定による方法に移り,ベイズの観点からのモデル選択と,これらを行うためのエビデンス近似を述べます.
もう一つの重要な教師あり学習である識別問題について学びます.
基本である線形の識別手法であるフィッシャーの判別分析やパーセプトロンをまず述べます. その後,生成モデルや識別モデルの考えと,具体的な手法を紹介します. この識別問題の場合でも,ベイズ推定の場合を紹介します.
代表的な機械学習の手法であるニューラルネットについて学びます.
ニューラルネット自体の紹介に続いて,誤差逆伝播法による学習について述べます. 勾配降下法による最適化と,そのために必要なヘッセ行列の近似を紹介します. このニューラルネットについても,正則化やベイズ推定の拡張をします.
データ集合 (データファイル@原著ホームページ),確率分布の一覧,行列の性質,変分法,ラグランジュ乗数
カーネル関数を適用するために必要な双対表現について述べてから,各種のカーネル関数を紹介します.その後,確率過程の一つであるガウス過程とカーネルの関連を示します.
サポートベクトルマシン(SVM)について学びます.
まず,マージン最大化の考えに基づいてSVMを導きます.その後,SVMのいくつかの問題点に対処した関連ベクトルマシンを紹介します.
グラフィカルモデル,特にベイジアンネットワークとマルコフ確率場について学びます.
ベイジアンネットワークやマルコフ確率場に代表されるグラフィカルモデルについて述べます.このモデルによる確率のモデル化と,その理解に必要な条件付き独立の概念を説明し,最後に,このモデルを用いた推論アルゴリズムを紹介します.
クラスタリング手法の一つであるk-means法についてふれたのち,混合ガウス分布をEMアルゴリズムによって解く方法を示します.その後,この混合ガウス分布とk-means法の関連など,EMアルゴリズムについて掘り下げます.
潜在変数間に複雑な関係がある場合の近似手法である変分ベイズ法などについて学びます.
確率の確定的な近似を行う変分ベイズ法とその具体的な計算例を示し,線形回帰やロジスティック回帰への適用について学びます.その後,もう一つの近似手法であるEP法を紹介します.
ギブスサンプリングなどの,確率的な近似手法について学びます.
最初に,与えられた確率分布に従ってサンプリングする基本手法を紹介します.その後,ギブスサンプリングやMetropolis-Hastings法などのマルコフ連鎖モンテカルロ法(MCMC)による確率的な近似手法について学びます.
主成分分析の確率的な定式化について学びます.
次元削減手法の代表である主成分分析を分散や誤差の観点から説明したのち,確率的主成分分析について学びます.因子分析やカーネル主成分分析など,その他の次元削減手法についても学びます.
隠れマルコフモデルと線形動的システムによる系列データの扱いについて学びます.
隠れマルコフモデルの推論手法であるViterbiアルゴリズムと,パラメータを推定するフォワード-バックワードアルゴリズムについて学びます.その後で,系列データを扱うための線形動的システムと粒子フィルタについて述べます.
コミッティやブースティングなど代表的なアンサンブル学習をまず紹介します.その後,決定木と,混合分布の拡張ともいえる混合エキスパートモデルについて学びます.